sjl623的杂货铺
0%

games101学习笔记1——Transformation

发表于 更新于 分类于 Valine：
本文字数： 7.9k 阅读时长 ≈ 7 分钟

最近在看games101，还挺有意思的，但是看完一遍之后发现很多看过的都忘了，所以决定尝试整理一份学习笔记。

以下是第一篇，关于Transformation。

Why Transformation

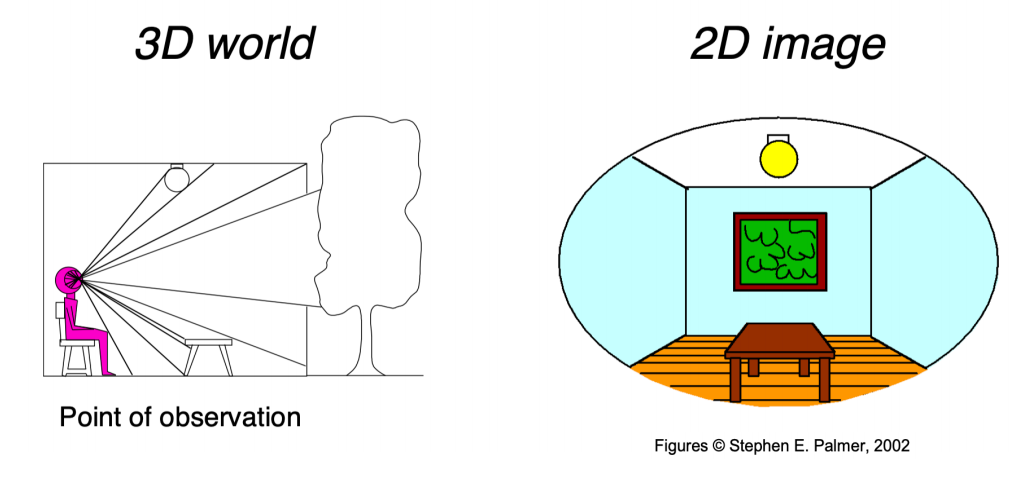
image-20211102005508970

2D Transformation

以下公式都默认为以(0,0)为原点的归一化坐标

Scale

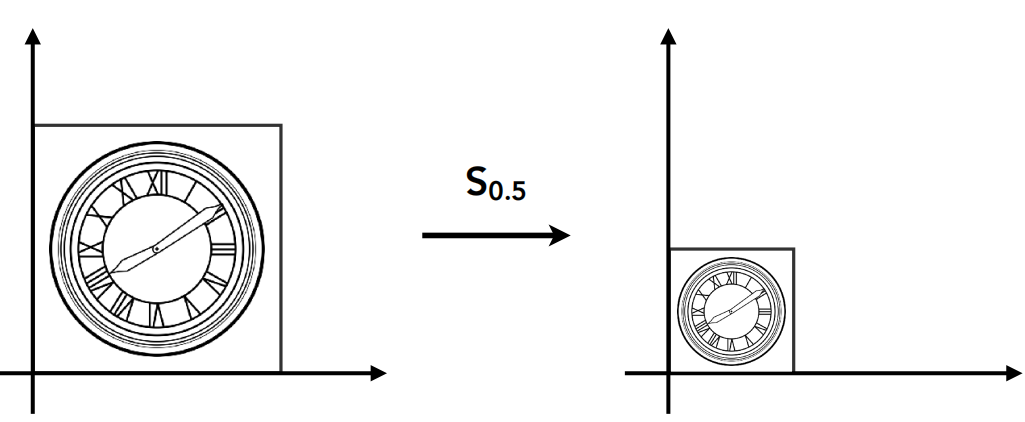
image-20211102005532596

若缩放s倍，则
$$
x^{‘}=sx
$$

$$
y^{‘}=sy
$$

表示为矩阵形式为：
$$
\left[
\begin{matrix}
x^{‘} \\
y^{‘} \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
s_{x} & 0\\
0 & s_{y} \\
\end{matrix}
\right]
\left[
\begin{matrix}
x\\
y\
\end{matrix}
\right]
$$
其中，$s_x$和$s_y$分别表示在x轴和y轴的缩放倍率

Reflection

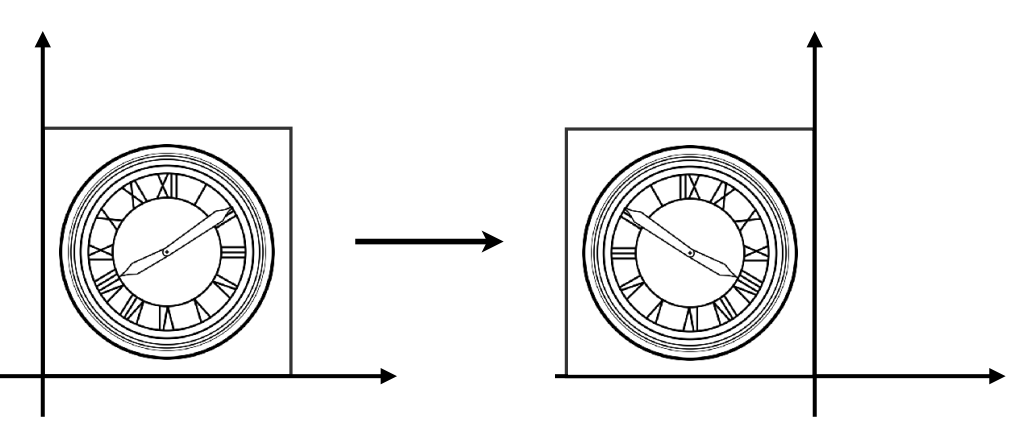
image-20211102005634820

矩阵形式
$$
\left[
\begin{matrix}
x^{‘}\\
y^{‘} \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
-1 & 0\\
0 & 1 \\
\end{matrix}
\right]
\left[
\begin{matrix}
x\\
y\
\end{matrix}
\right]
$$

Shear(错切)

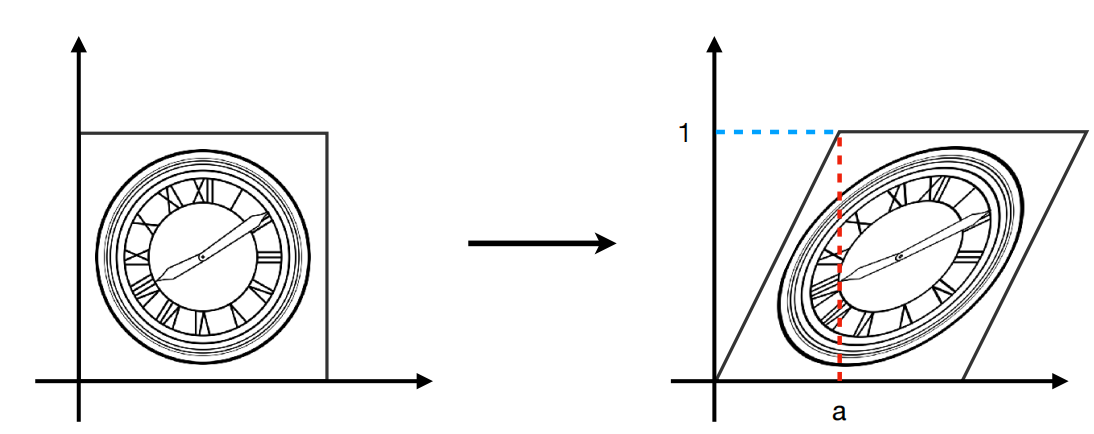
image-20211102005937524

  • 垂直方向位移为0
  • 水平方向y=0处位移为0
  • 水平方向y=1处位移为a

矩阵形式
$$
\left[ \begin{matrix} x^{‘}\\ y^{‘} \ \end{matrix} \right]
=\left[ \begin{matrix} 1 & a\\ 0 & 1 \ \end{matrix} \right]
\left[ \begin{matrix} x\\ y\ \end{matrix} \right]
$$

Rotate

绕原点，顺时针$\theta$°

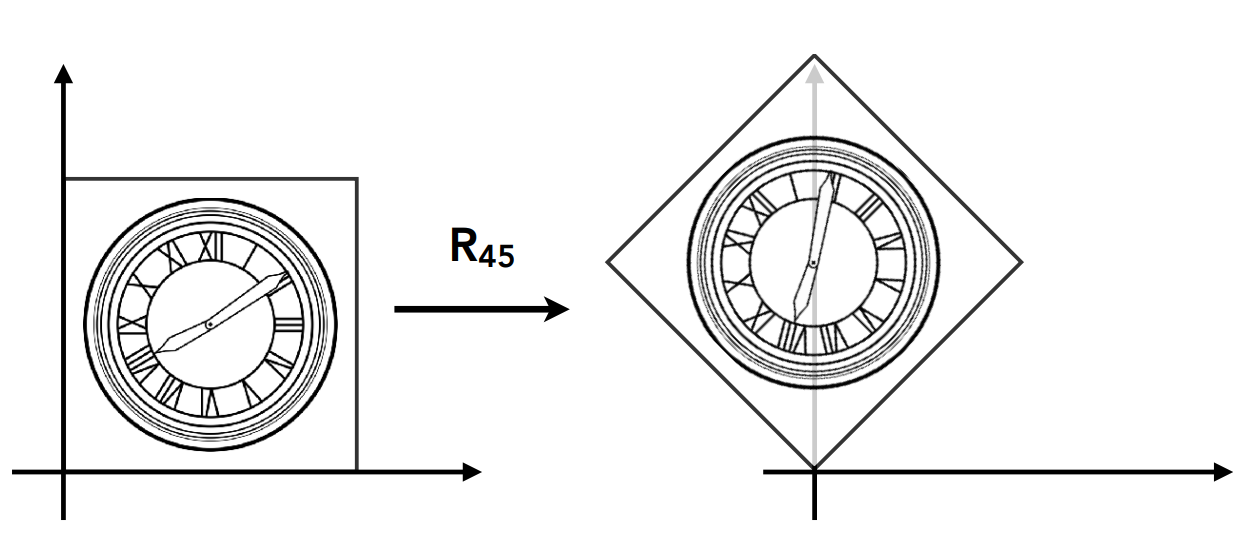
image-20211106022135391

分别以(0,1)和(1,0)特殊点代入，有

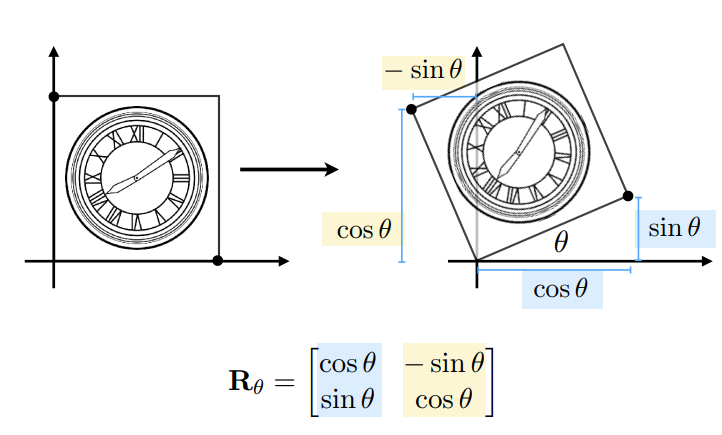
image-20211106022203119

即
$$
R_{\theta}=\left[ \begin{matrix} cos{\theta} & -sin{\theta}\\ sin{\theta} & cos{\theta} \ \end{matrix} \right]
$$

若旋转$-\theta $°，则
$$
R_{-\theta}=\left[ \begin{matrix} cos{\theta} & sin{\theta}\\ -sin{\theta} & cos{\theta} \ \end{matrix} \right] = R_\theta^T
$$
即旋转$\theta$和$-\theta$度的变换矩阵有如下关系：$R_{\theta}^T = R_{\theta}^{-1}$ ，即是正交矩阵

Linear Transforms

$$
x^{‘}=ax+by
$$

$$
y^{‘}=cx+dy
$$

表示为矩阵形式：
$$
\left[ \begin{matrix} x^{‘}\\ y^{‘} \ \end{matrix} \right]=\left[ \begin{matrix} a & b\\ c & d \ \end{matrix} \right]\left[ \begin{matrix} x\\ y\ \end{matrix} \right]
$$

Homogeneous coordinates(齐次坐标)

Why Homogeneous Coordinator

Translate(平移变换)：

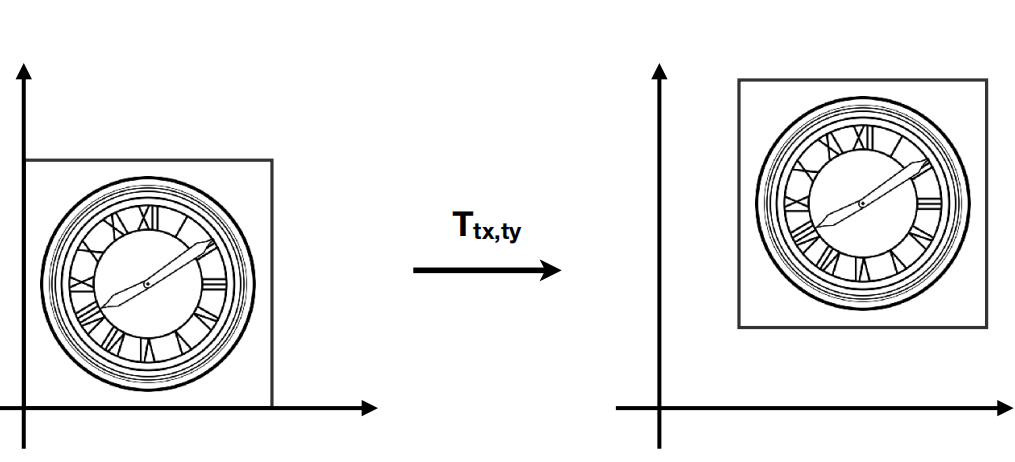
image-20211102011114467
$$
x^{‘}=x+t_x\
$$

$$
y^{‘}=y+t_y
$$

不能表示为线性变换，因为平移是形如$\left[ \begin{matrix} x^{‘}\\ y^{‘} \ \end{matrix} \right]=\left[ \begin{matrix} a & b\\ c & d \ \end{matrix} \right]\left[ \begin{matrix} x\\ y\ \end{matrix} \right]+\left[ \begin{matrix} t_x\\ t_y\ \end{matrix} \right]$的形式

为了能够通过矩阵统一表示仿射变换，故引入齐次坐标。m

即：

  • 平面上的一点表示为 $(x,y,1)^T$
  • 平面上的向量表示为$(x,y,0)^T$
  • 抽象为$(x,y,w)^T$代表点$(x/w,y/w)$，当w为0时变为向量

进而平移可以表示为：
$$
\begin{pmatrix} x^{‘}\\ y^{‘}\\ w^{‘} \ \end{pmatrix}=\begin{pmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y \\ 0 & 0 & 1\ \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \ \end{pmatrix} = \begin{pmatrix} x+t_x\\ y+t_y \\ 1 \ \end{pmatrix}
$$

没有免费的午餐：增加了计算量和存储空间

齐次坐标的精妙之处(w-coordinate 0/1->vector/point)：

  • vector + vector = vector
  • point - point = vector
  • point + vector = point
  • point + point = ??

Affifine Transformations 仿射变换

Affifine map = linear map + translation （仿射变换 = 线性变换 + 平移）
$$
\begin{pmatrix} x^{‘}\\ y^{‘} \ \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \ \end{pmatrix} \begin{pmatrix} x\\ y \ \end{pmatrix} + \begin{pmatrix} t_{x}\\ t_{y} \ \end{pmatrix}
$$
齐次坐标下有：
$$
\begin{pmatrix} x^{‘}\\ y^{‘}\\ 1 \ \end{pmatrix}=\begin{pmatrix} a & b & t_x\\ c & d & t_y \\ 0 & 0 &1\ \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \ \end{pmatrix}
$$

2D Transformation

Scale

$$
S_{(s_x,s_y)}=\begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix}
$$

Rotation

$$
R_{(\alpha)}=\begin{pmatrix} cos\alpha & -sin\alpha & 0 \\ sin\alpha & cos\alpha & 0 \\ 0 & 0 & 1 \end{pmatrix}
$$

Translation

$$
T_{(t_x,t_y)}=\begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix}
$$

Inverse Transform

$M^{-1}$是矩阵$M$的逆变换

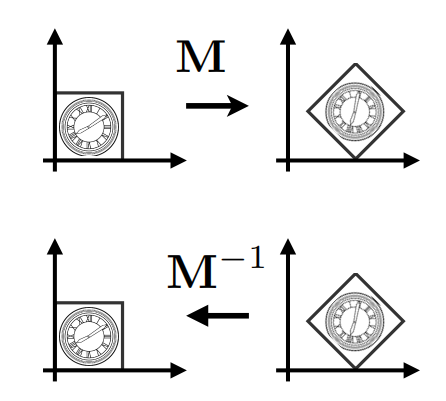
image-20211102221849411

Composite Transform

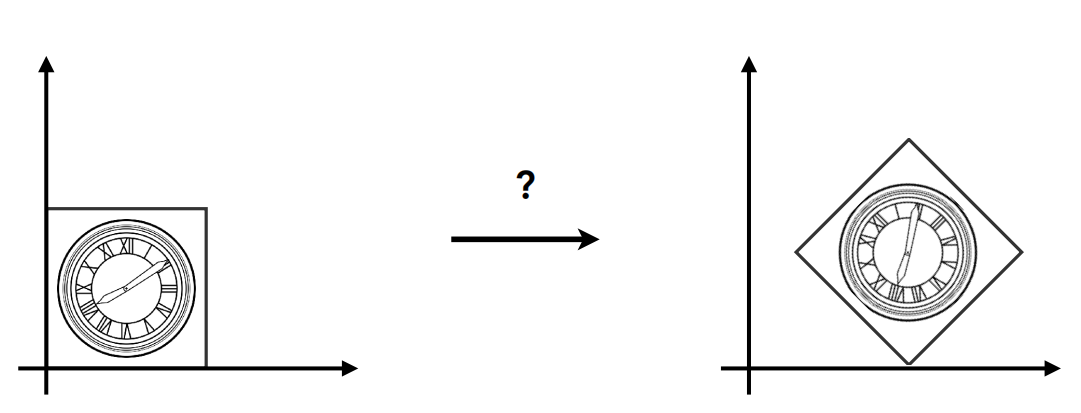
image-20211102222036505

平移和旋转先后问题

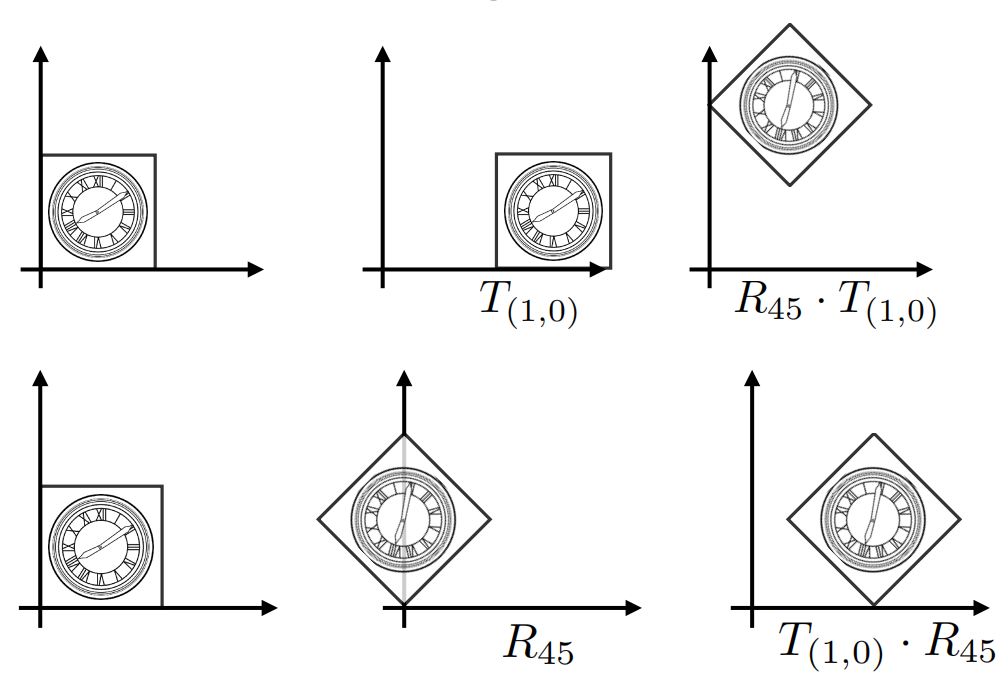
image-20211102222107669

  • 由于旋转是绕原点的，故应先旋转再平移

$$
T_{1,0}\cdot R_{45}\left[ \begin{matrix} x\\ y \\1 \ \end{matrix} \right]=\left[ \begin{matrix} 1 & 0 & 1\\ 0 & 1 & 0 \\ 0 & 0 & 1 \ \end{matrix} \right]\left[ \begin{matrix} cos45^{\circ} & -sin45^{\circ} & 0\\ sin45^{\circ} & cos45^{\circ} & 0 \\ 0 & 0 & 1 \ \end{matrix} \right]\left[ \begin{matrix} x\\ y\\ 1 \end{matrix} \right]
$$

  • 矩阵运算满足结合律，可据此调整运算顺序减少运算量
  • 绕某个点旋转
    • 平移到原点
    • 旋转
    • 平移回去
    • $T(c) \cdot R(\alpha) \cdot T(-c)$

3D Transformation

$$
\begin{pmatrix} x^{‘}\\ y^{‘}\\ z^{‘} \\ 1 \ \end{pmatrix}=\begin{pmatrix} a & b & c & t_x\\ d & e & f& t_y \\ g & h & i & t_z\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \ \end{pmatrix}
$$

对应的，

Scale矩阵为：
$$
S_{(S_x,S_y,S_z)}=\begin{pmatrix} s_x & 0 & 0 & 0\\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}
$$
Translation矩阵为：
$$
S_{(S_x,S_y,S_z)}=\begin{pmatrix} 1 & 0 & 0 & t_x\\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z\\ 0 & 0 & 0 & 1 \end{pmatrix}
$$
三维绕轴旋转公式：
$$
R_x(\alpha)=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & cos\alpha & -sin\alpha & 0 \\ 0 & sin\alpha & cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}
$$

$$
R_y(\alpha)=\begin{pmatrix} cos\alpha & 0 & sin\alpha & 0\\ 0 & 1 & 0 & 0 \\ -sin\alpha & 0 & cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}
$$

$$
R_z(\alpha)=\begin{pmatrix} cos\alpha & -sin\alpha & 0& 0\\ sin\alpha & cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}
$$

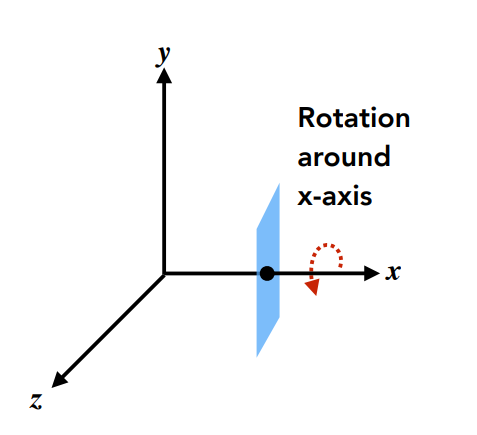
image-20211106025937373

为什么绕y轴旋转是负的？这里首先要区分清楚一个问题，就是角度的正负。旋转$\alpha$°当$\alpha$大于0时是往哪个方向旋转？答案是从所绕轴的负方向看过去的顺时针。这个可以这么理解：有一张纸，中间插着一根木棍，通过木棍(y轴)可以旋转纸张，这个时候按顺时针旋转就是从X往Z的方向转对吧。但是Y方向却是由$Z \times X$得来的，刚好相反。而我们前面定义的二维平面旋转矩阵$R_{\theta}=\left[ \begin{matrix} cos{\theta} & -sin{\theta}\\ sin{\theta} & cos{\theta} \ \end{matrix} \right]$指的也应该是从右手中四指所指轴出发往另一轴方向转$\theta$°时的变换。也就是说Y方向比较特殊，从旋转α°的角度来解释，这里的α>0按照表示习惯指的应该是所绕轴的负方向看过去的顺时针转过的度数，和我们定义旋转变换矩阵时所定义的方向恰好相反了，所以应该取$\theta = -\alpha$代入。可以验证一下绕X轴和Z轴时的情景会发现，这时候则是“所绕轴的负方向看过去的顺时针方向”与”右手中四指所指轴出发往另一轴方向“的方向是一致的。

3D Rotations

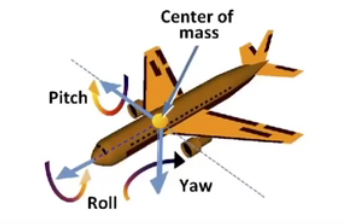
image-20211106223723605

$$R_{xyz}(\alpha,\beta,\gamma)=R_x(\alpha)R_y(\beta)R_z(\gamma)$$

一个向量绕一个轴$n$旋转$\alpha$°的变换矩阵(Rodrigues' Rotation Formula)写做：$R(n,\alpha)=cos(\alpha)I + (1 - cos\alpha))nn^{T} + sin(\alpha)\begin{pmatrix} 0 & -n_z & n_y\\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix}$

其中需要注意：

  • 该公式假定绕以原点为起点，沿向量$n$方向旋转
  • 如果需要沿着任意轴旋转，则先平移到原点（向量、旋转点都平移），然后旋转，再平移回去

四元数

  • 便于旋转插值

View/Camera Transformation

  • What is view Transformation?(类比拍照)
    • 摆好物体(Model transformation)
    • 找一个角度(View transformation)
    • 拍照(Projection transformation)

View transformation

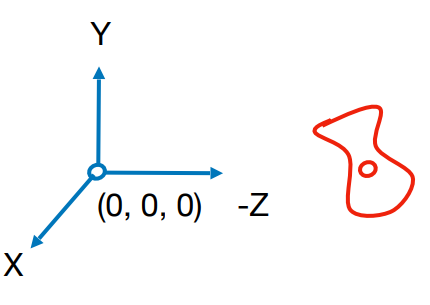
image-20211107174103021

关键点：

  • 假设相机摆放在原点，向上方向为y，朝着-z方向看
  • 其余物体相对移动

通过$M_{view}$矩阵变换，实现场景中的其他物体也相对的移动到摄像机在原点，往-z方向看，向上方向为y时的坐标(关于向上方向，想象一下头上有根天线，歪头看向一个方向，天线所指的方向🤣)

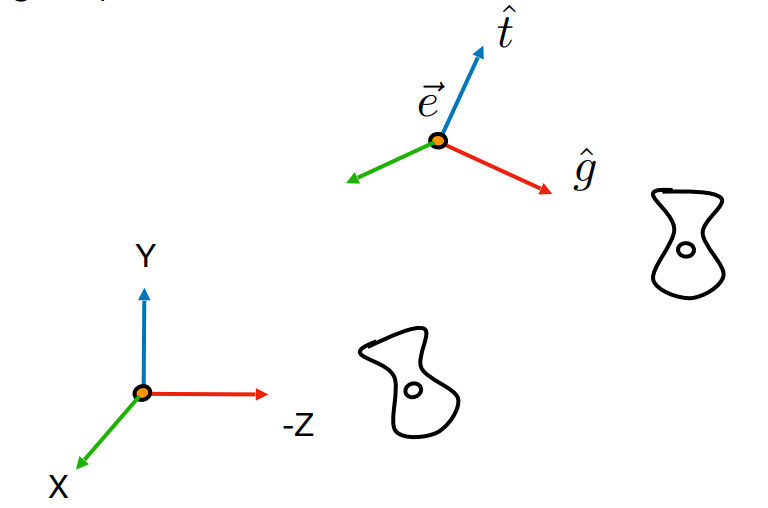
image-20211107180905691

则$M_{view}$需要表示

  • 将$\vec{e}$移到原点
  • 旋转$\hat{g}$到-Z方向
  • 旋转$\hat{t}$到Y方向
  • 旋转$(g \times t)$到X方向

记$M_{view}=R_{view}T_{view}$(先平移再旋转)

则$T_{view}=\left[ \begin{matrix} 1 & 0 & 0 & -x_e\\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 &-z_e \\ 0 & 0 & 0 & 1 \end{matrix} \right]$

接着考虑写出$R_{view}$

$R_{view}$变换并不容易直接写出，则考虑逆变换

想象已经转好了的坐标(1,1,1)，需要将其转回去，也就是施加$R_{view}^{-1}$的变换，则有$R_{view}^{-1}=\left[ \begin{matrix} x_{g \times t} & x_t & x_{-g} & 0\\ y_{g \times t} & y_t & y_{-g} & 0 \\ z_{g \times t} & z_t & z_{-g} & 0 \\ 0 & 0 & 0 & 1\end{matrix} \right]$（想象将$I$施加$R_{view}^{-1}$变换即可理解$R_{view}^{-1}$是怎么得来的)，既然逆变换有了，又因为旋转矩阵是正交矩阵，则直接将$R_{view}^{-1}$转置就可以得到$R_{view} =\left[ \begin{matrix} x_{g \times t} & y_{g \times t} & z_{g \times t} & 0\\ x_{t} & y_t & z_{t} & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1\end{matrix} \right]$

Projection transformation

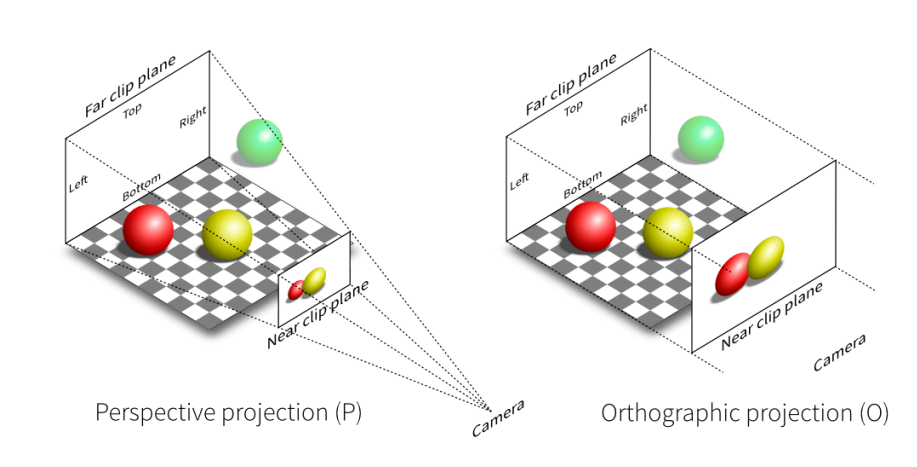
image-20211107233128219

Orthographic Projection

平行投影的理解：

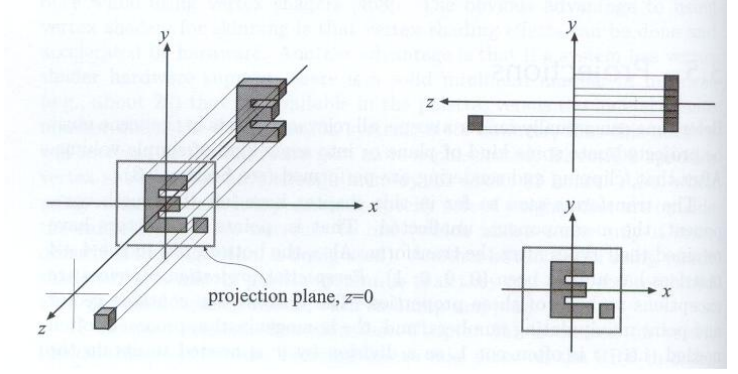
image-20211108004231806

  • 相机位于原点，看向-z方向，向上方向为y
  • 将z轴坐标丢掉
  • 正则化

对于一个目标空间范围$[l,r] \times [b,t] \times [f,n]$，首先需要映射到正则(canonical)立方体$[-1,1]^3$中

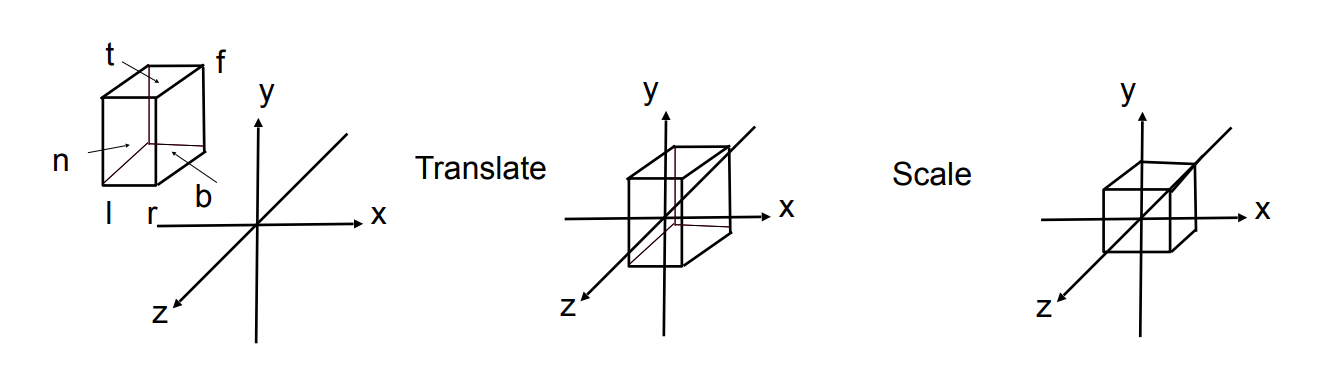
image-20211108004509157

具体步骤为：

  1. 将中点移到原点
  2. 缩放

$$
M_{ortho} =\left[ \begin{matrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} &0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]\left[ \begin{matrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{matrix} \right]
$$

做完变换会拉伸，后续还有视口变换

Perspective Projection

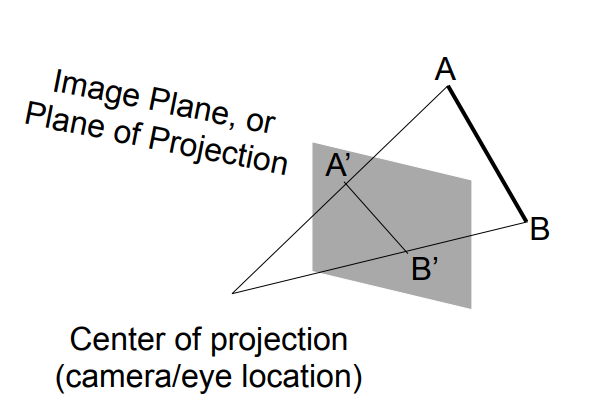
image-20211108010811780

如何实现透视投影？

  1. 将锥体(frustum)挤成长方体(cuboid)
  2. 进行正交投影(orthographic projection)

关键在于第一步

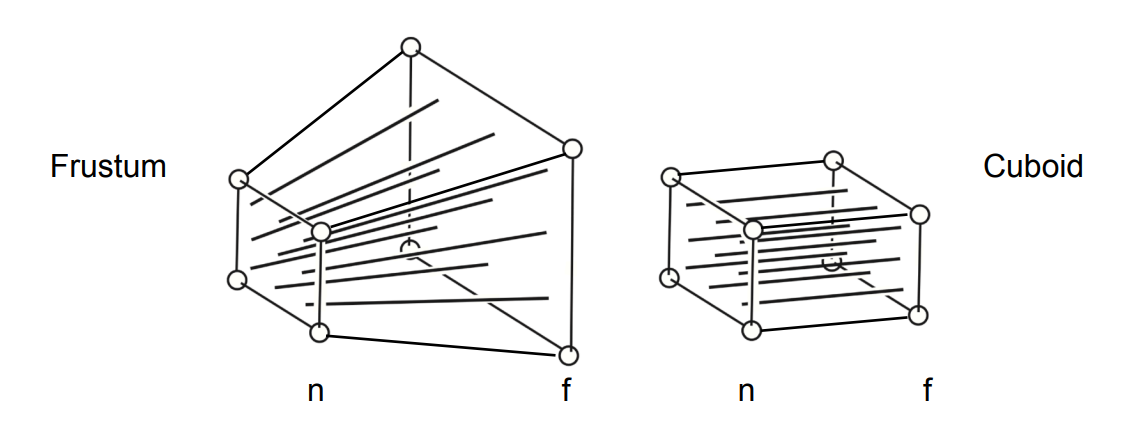
image-20211108012113841

特点：

  1. 近平面四个点不动
  2. 远平面z值不变
  3. 远平面的中心点不会发生变化

寻找映射前后的($x$,$y$,$z$)和($x^{‘}$,$y^{‘}$,$z^{‘}$)的关系

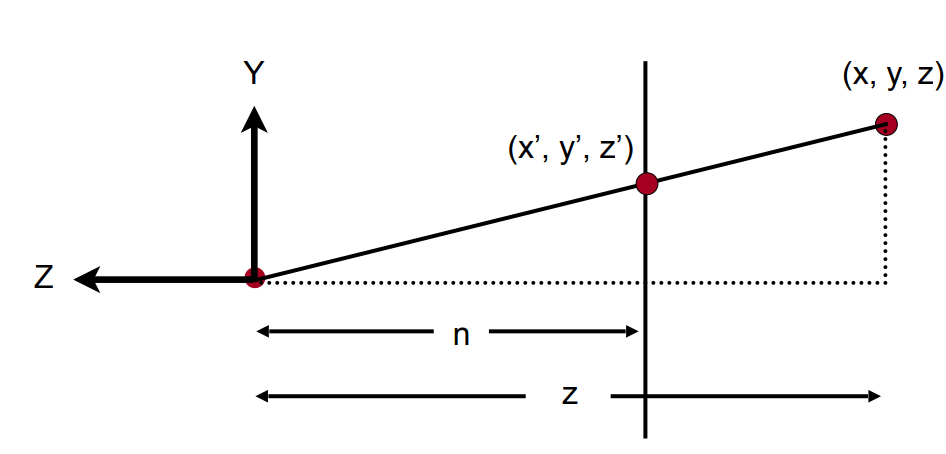
image-20211108013034460

由相似三角形可以得到$y^{‘}=\frac{n}{z}y$,类似的$x^{‘}=\frac{n}{z}x$

也就是对于齐次坐标下的一个点$\begin{pmatrix} x\\ y\\ z \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} nx/z\\ ny/z\\ ? \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} nx\\ ny\\ ? \\ z \end{pmatrix}$

则可以初步确定$M_{persp \rightarrow ortho} = \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0 \\ ? & ? & ?& ?\\ 0 & 0 & 0 & 1 \end{pmatrix}$

剩下的问题是确定z的变换关系，依据

  • 在近平面的点z值不变
  • 在远平面的点z值不变

可得$\begin{pmatrix} x\\ y\\ n \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} nx\\ ny\\ n^2 \\ z \end{pmatrix}$，$\begin{pmatrix} 0\\ 0\\ f \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} 0\\ 0\\ f^2 \\ f \end{pmatrix}$

即矩阵第三行一定为$(0,0,A,B)$的形式，且可以列出方程
$$
\begin{cases} An+B=n^2\\ Af+B=f^2 \end{cases} \Rightarrow \begin{cases} A=n+f\\ B=-nf \end{cases}
$$
至此，$M_{persp \rightarrow ortho}$已经求得

接着即可做平行投影，即最终$M_{persp} = M_{ortho}M_{persp\rightarrow ortho}$